Split mid term in 7 seconds

Quadratic expressions of the form ax2 + bx + c, where a, b, and c are constants, can be factored using the split mid term in 7 seconds. The strategy entails splitting the middle term bx into two terms so that when you add or subtract them, you receive middle term bx, and when you multiply them, you get the product of the first and last terms ac. Once the first two terms and the last two terms have been grouped independently, the expression can then be factored by removing the common factors. Most often, while trying to represent the first and final terms as a middle term by adding or subtracting, students get stuck trying to discover the two factors of the product of the first and last terms. It takes longer to do this. Web Tutors Point recognized the issue and offered the fastest technique to identify the two ideal mid term factors in just 7 seconds.
Chapter 13 (Factorization) of Maths in 8th class is crucial with regard to all tests. Splitting the middle term is an essential strategy for factoring quadratic equations, hence it is crucial for all students to learn. Quadratic equation factoring is a fundamental algebra technique that is applied in many branches of science and mathematics. Students can factor quadratic expressions more quickly and effectively by understanding how to split the middle term, which can aid in problem-solving. Furthermore, mastering more complex algebraic concepts like resolving systems of equations and graphing quadratic functions requires a solid foundation in factoring quadratic equations. Therefore, if a student wants to succeed in algebra and beyond, knowing the method of splitting the middle term is crucial. Here, WTP attempted to clarify the simplest way to identify the two factors that most students struggle with.
Steps to split mid term in 7 seconds
The steps to factorize using the split mid-term approach are as follows:
Step 1: Find the first and last term’s product, and you’ll obtain an ac as a result.
Step 2: Identify two ac factors that together sum to b.
Step 3: The two factors from step 2 can be added or subtracted to rewrite the middle term, bx.
Step 4: Separately, combine the first and last two terms.
Step 5: Take out the common factors from each group.
Step 5: The final factorization is obtained by combining the two components.
For example, let’s factorize the expression 2x2 + 5x + 3 using the split mid-term method:
Step 1: Multiplying first and last terms 2x2 and 3 = 2x2 x 3 = 6x2
Step 2: Finding two factors of 6x2 that add up to 5x (middle term in this case):
The table below can be used to quickly find two factors:
As shown below, we will verify all the numbers between 1 and 9 that divide 6 and then write the divisor in the first row and the quotient in the second row:
1 | 2 |
6 | 3 |
As you can see, when you add 2 and 3, you obtain the middle term 5, thus we’ll take these two factors into account.
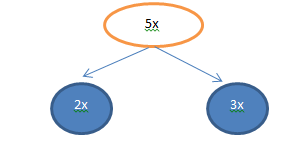
Step 3: Rewrite 5x as 2x + 3x so equation will be 2x2 + 2x + 3x + 3.
Step 4: Group the first two terms and the last two terms: (2x2 + 2x) + (3x + 3).
Step 5: Factor out the common factors from each group: 2x(x + 1) + 3(x + 1).
Step 6: Combine the two factors to get the final factorization: (2x + 3)(x + 1).
Therefore, the factorization of 2x2 + 5x + 3 using the split mid-term method is (2x + 3)(x + 1).
