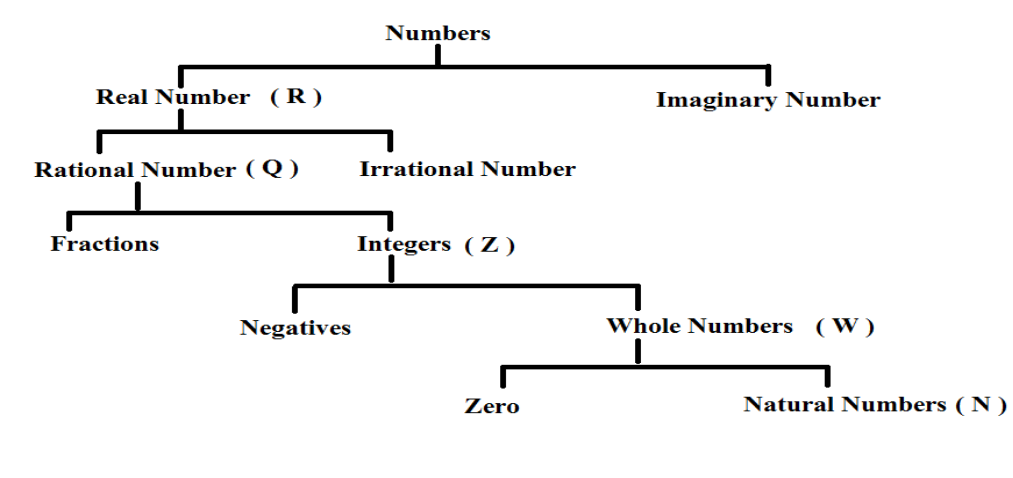
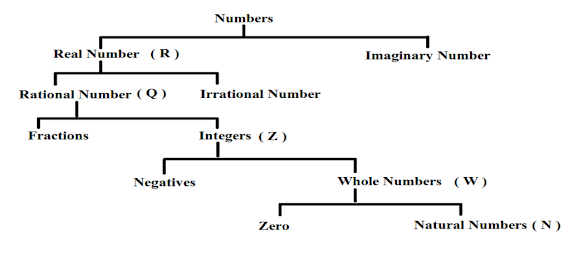
After reading Classification of the Number System, we could distinguish between real and imaginary numbers. Reading History of Number System & Number System is advised if you haven’t previously. We will learn in-depth classification of numbers in this part.
Let’s analyze the Classification of numbers.
Depending on their characteristics and methods of representation, numbers can be divided into many categories. Here are some of the most typical categories for numbers:
Natural Number (N)
In order to count items or tangible things, natural numbers are employed. It’s also known as a counting number. At 1, a countdown starts that never stops. The smallest natural number is 1, and the greatest natural number is unknown as a result. The numbers 1, 2, 3, 4, 5, 6, 7, etc. are all natural numbers. It is symbolized by N.
Consecutive Natural Numbers are the natural numbers that come after one another and are distinct from one another by 1. If y is any natural number, then y+1, Y+2, Y+3, etc. are the natural numbers that follow y.
Natural Numbers on Number Line:
Even Natural Numbers
An even natural number system is a group of natural numbers that may be multiplied by two or are divisible by two. E= (2,4,6,8,10,12, etc.) is an example. Even numbers can go on forever.
Odd Natural Numbers
Any group of natural numbers that cannot be divided by two is said to be a “odd natural number.” O=(1,3,5,7,9,…) is an example of Odd Natural Number. The odd numbers are infinite.
A collection of both odd and even integers is what is known as a natural number.
Whole Numbers (W)
Whole numbers are collection of zero and natural numbers. Whole Numbers = Set of 0 and Natural Numbers = {0, 1, 2, 3, 4, 5, 6,…, etc.}. The smallest whole number is zero, but there is no means to get to the greatest whole number. Following whole numbers differ by 1.
Every even natural number is also an even whole number. Additionally, each odd natural number is an odd whole number.
Integers (Z)
Positive, negative, or zero are all possible values for an integer. A fractional number is not allowed. It is denoted by Z or I.
In other words, Z or I =…, -3, -2, -1, 0, 1, 2, 3,…
Additionally, both the positive and negative sides include infinite integers. All of the natural numbers are positive integer.
Application of Integers in Real Life
We use integers to represent our everyday situations mathematically.
- Positive numbers are used to indicate credit, whereas negative integers are used to represent debit.
- Positive integers are used to indicate profits while negative numbers are used to represent losses.
- If heights above sea level are positive integers, then depths below sea level are defined by negative numbers.
- Integers with positive signs denote price increases, those with negative signs denote price declines, and so on.
Some numbers may fit into more than one category. For instance, 5 is a whole number, an integer, a natural number, and a rational number.
Prime Numbers
Prime numbers are whole numbers that can only be divided by one and by themselves and are bigger than one. In contrast to 2, all prime numbers are odd. P= 2,3,5,7,11,13,………. etc.
Since there are only two factors for prime numbers—the number itself and the number 1, respectively—both of these factors must be distinct from one another. As an illustration, if we look at 1, we can only find the factors 1 and 1, as they are identical. It is not a prime number, therefore.
Composite Numbers
The term “Composite Number” refers to a whole number (greater than 1) that is not a prime. A composite number C = (4, 6, 8, 9,…)
Fractions
A fraction or fractional number is used to represent a piece of a whole or, more broadly, any number of equal parts.
Fractions consist of a denominator (which is below the line) and a numerator (which is above the line). It may be expressed as p/q, where p and q are both whole numbers and q is not equal to 0.
Kinds Of Fractions
Proper Fraction:
The fraction in which the numerator is smaller than the denominator called Proper Fraction, for instance 3/4, here numerator 3 is smaller than denominator 4.
Improper Fraction:
The fraction in which the numerator is superior to the denominator called Improper Fraction, for instance 9/2. Here numerator is greater than the denominator.
Mixed Fraction or Mixed Numeral:
It is composed of a whole part and a proper fraction, for instance 2 and 1/3.
Equivalent Fractions:
Fractions that keep on the same proportion of another fraction, for instance: 5/2=10/4 both indicates 5/2 if simplified.
Irreducible Fraction:
It cannot be simplified, it means there is no number common between numerator & denominator other than 1, for instance: 4/3 .
Decimal Fraction:
The denominator is a power whose base is 10 (10,100,1000,…), for instance 8/100.
Ratios
A ratio is a relationship between two or more numbers that can be sometimes expressed as a fraction. Typically, a number of items are grouped and compared in a ratio, specifying numerically the relationship between each group. Ratios are expressed as “group 1 to group 2—to group n”.
For example, if a car lot had 12 vehicles, of which 2 are white, 6 are red, and 4 are yellow, then the ratio of red to white to yellow cars is 6 to 2 to 4.
The ratio of yellow cars to white cars is 4 to 2 and may be expressed as 4:2 or 2:1.
A ratio is often converted to a fraction when it is expressed as a ratio to the whole. In the above example, the ratio of yellow cars to all the cars on the lot is 4:12 or 1:3. We can convert these ratios to a fraction and say that 4/12 of the cars or ⅓ of the cars in the lot are yellow.
Rational Numbers (Q)
A rational number is a number that can be in the form p/q where p and q are integers and q is not equal to zero. For e.g., 3/4, -2/7, etc.
Difference between Fraction and Rational Number
A fraction is any number of the form a/b where both “a” and “b” are whole numbers {0,N} and b≠0.
On the other hand, a rational number is a number which is in the form of p/q where both “p” and “q” are integers and q≠0
Any number that can be written in fraction form is a rational number. This includes integers, terminating decimals, and repeating decimals as well as fractions.
An integer can be written as a fraction simply by giving it a denominator of one, so any integer is a rational number.
Every fraction is a rational number but a rational number need not be a fraction.
Let a/b be any fraction. Then, a and b are natural numbers. Since every natural number is an integer. Therefore, a and b are integers. Thus, the fraction a/b is the quotient of two integers such that b ≠ 0.
Hence, a/b is a rational number.
We know that 2/-3 is a rational number but it is not a fraction because its denominator is not a natural number.
Irrational Number
Irrational number is a real number that cannot be written as a simple fraction. Irrational means not Rational.
Irrational numbers can also be expressed as non-terminating and non-recurring (continued fractions) decimal, that cannot be written in the form p/q where p and q both are integers and q is not equal to 0.
When expressed as a decimal, irrational numbers go on forever after the decimal point and never repeat.
e.g π (Pi) is a famous irrational number.
The most famous irrational number is sqrt(2), sometimes called Pythagoras’s constant.
A proof that the square root of 2 is irrational:
Let’s suppose √2 is a rational number.
Then we can write it √2 = a/b where a, b are integers, b not zero.
We additionally assume that a/b is simplified to lowest terms, it means both of a and b cannot be even. One or both must be odd.
From the equality, √2 = a/b => 2 = a^2/b^2, or a^2 = 2 · b^2.
So, the square of a is an even number since it is two times something.
From this we know that a itself is also an even number.
Because it can’t be odd; if a itself was odd, then a · a would be odd too. Odd number times odd number is always odd.
If a itself is an even number, then a is 2 times some other whole number.
If we substitute a = 2k into the original equation 2 = a^2/b^2, this is what we get:
2 = (2k)^2/b^2
2 = 4k^2/b^2
2*b^2 = 4k^2
b^2 = 2k^2
This means that b^2 is even, from which follows again that b itself is even. And that is a contradiction!!!
Because we started the whole process assuming that a/b was simplified to lowest terms, and now it turns out that a and b both would be even. We ended at a contradiction; thus our original assumption (that √2 is rational) is not correct.
Therefore √2 cannot be rational. It’s irrational number.