Criss-Cross Method (Fastest Method of Multiplication): A Vedic Mathematical Trick
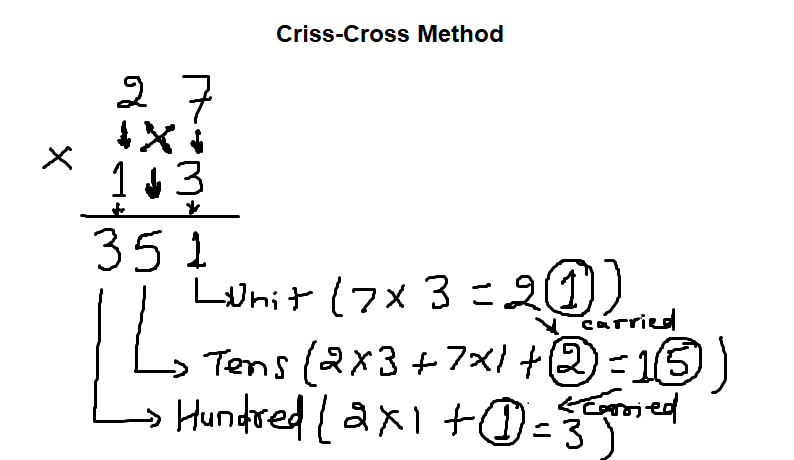
Vedic Mathematics works for every combination of numbers of any length with the same accuracy as the old method of multiplication while also assisting us in obtaining the solution much more quickly. In the “Urdhva-Tiryak Sutra,” a method of multiplication (Criss-Cross multiplication) is described, it means “vertically and cross-wise.” This method of multiplication is known as the Criss-Cross system of multiplication or lattice method.
3 Steps to Get the answer much faster
Steps for multiplication of 2 two digits numbers:
1. Multiply the digits in the ones place, write in the ones place of the answer. For instance, if you multiply the unit digits 3 and 3 of the integers 23 and 13 together, you will get the unit place digit in the multiplication shown below.
2 3
X
1 3
______________
Unit digit of product = (3 x 3)
2. Cross multiply and add the products, write in the tens place of the answer.
2 3
X
1 3
______________
Tens digit = (3 x 2 + 1 x 3); Unit Digit = 9
3. Multiply the tens digits, write in the hundred place of the answer.
2 3
X
1 3
______________
Hundred Digit = (2 x 1); Tens Digit = 9; Unit Digit = 9
Hence,
2 3
X
1 3
______________
2 (3* 2 + 1 * 3) 9
= 2 (6 + 3) 9
= 299 is the answer.
Let’s consider another example, 23 x 17
2 3
X
1 7
______________
Hundred Digit: {(2 x 1) = 2 + Carried digit from tens place};
Tens Digit: {(7* 2 + 1 * 3) = (14 + 3 = 17) + Carried digit from Unit Place};
Unit Digit: (3 x 7 = 21)
= {(2) + Carried Digit};{(14 + 3)+2} ;1
= (2 + 1); 9; 1
= 391
Steps for multiplication of 2 three digits numbers:
Step 1: Multiply Unit Digits
a b c
| (c X z)
x y z
Step 2: Cross multiply unit and tens digits and add their products.
a b c
( b x z) + ( c x y )
x y z
Step 3: Cross multiply unit and hundred place digits, then add their products with tens digits product, as shown below:
a b c
(a x z) + ( c x x )+ ( b x y)
x y z
Step 5: Cross multiply tens and hundred digits and add their products.
a b c
( a x y) + (b x x)
x y z
Step 6: Finally multiple hundred digits.
a b c
( a x x)
x y z
Let’s understand by an example,
1 3 2
X 1 2 1
Ten Thousand: (1 x 1); Thousand: {(1×2) + ( 3×1)}; Hundred: {(1×1)+(2×1)+(3×2)}; Tens: {(3×1) + (2 x2)}; Unit: (2 x 1)
= 1 5 ,9 7 2 is the answer.
Let’s try another example with carry,
2 3 4
X 1 2 3
Ten Thousand: (2) + Carried Digit, Thousand: (4+3) + Carried Digit, Hundred: (6+4+6) + Carried Digit, Tens: (9+8) + Carried Digit, Unit: (12)
= 2 + C, 7 + C, 16 + C, 17 + 1; 2 ( Here, C depicts Carried digit)
= 2 + C, 7 + C, 16 + 1; 8; 2
= 2 + C, 7 + 1; 7; 8; 2
= 28, 782
It follows that the Criss-Cross method is the quickest way to calculate the outcome of multiplying two integers or three digit numbers.
How the Criss-Cross method, also known as lattice multiplication, can be useful in competitive exams?
For a number of reasons, the Criss-Cross approach, commonly referred to as lattice multiplication, might be helpful in competitive exams:
Efficiency: For large numbers, lattice multiplication frequently outperforms conventional long multiplication in terms of speed. Being able to complete calculations more rapidly might be a huge benefit during time-limited competitive exams.
Accuracy: When compared to more complex approaches, the criss-cross method’s systematic design makes mistakes less likely to occur. In competitive tests, accuracy is essential because even minor errors can lose you points.
Simple And Easy to learn: The technique is fairly straightforward to master. When taking an exam under pressure and having to make exact calculations when pressed for time, this might be especially helpful. The Criss-Cross approach requires students to carefully examine place value. This improves their comprehension of place value, a crucial idea in mathematics.
Sequential Process: The Criss-Cross method is a straightforward step-by-step process that can keep you organized and engaged while taking the test. In order to decrease the likelihood of making mistakes, difficult multiplication problems can be broken down into simpler parts.
Visual Aid: The grid layout of lattice multiplication offers a visual aid that can help you keep track of your computations. When working with numbers with multiple digits, this is particularly useful.
Wide Range: A wide variety of multiplication problems, including those involving multiple digits and decimals, can be solved using lattice multiplication. Knowing a flexible technique like lattice multiplication can be useful because you might come across several sorts of multiplication questions in competitive exams.
Confidence: Being confident throughout the exam can be increased by having a variety of strategies for completing mathematics problems. You have another mathematical weapon at your disposal if you are familiar with the criss-cross method.
Problem-Solving Techniques: Lattice multiplication promotes problem-solving techniques and critical thinking, which are beneficial for both multiplication and other mathematical ideas that may occur in competitive exams. The Criss-Cross method promotes problem-solving abilities and critical thinking by breaking down multiplication into smaller steps and patterns.
Even if adopting the Criss-Cross approach can be helpful in competitive tests, it is crucial to practice and become an expert first. Knowing the technique well will enable you to take full use of its advantages during the exam. Web Tutors Point explains this approach to help students in competitive exams answer problems accurately and fast.
