Divide polynomial in 7 seconds
Dividing a polynomial by another is known as algebraic division. Algebraic expression division is comparable to number division. We get the residual and the quotient when we divide a number. In a similar vein, the remainder and quotient are obtained when dividing algebraic expressions. The algebraic long method, also known as the conventional method of dividing algebraic expressions, is the most widely used of the three methods available for dividing polynomials: the long division method, factorization method and synthetic division method. Here we will learn all these 3 effective ways to divide polynomial in 7 seconds.
The Long Division Method
Mantra: Divide the first term of the dividend (the polynomial to be divided) by the first term of the divisor. This gives the first term of the quotient.
Here are the steps in dividing polynomials using the long division method:
Step 1: Arrange the polynomial in descending order based on their variable powers. Replace the missing term(s) with 0.
Step 2:
Divide the first term of the dividend (the polynomial to be divided) by the first term of the divisor. This gives the first term of the quotient.
Step 3: Multiply the divisor by the first term of the quotient.
Step 4: Subtract the product from the dividend then bring down the next term. The difference and the next term will be the new dividend.
Note: Remember the rule in subtraction “change the sign of the subtrahend then proceed to addition”.
Repeat step 2-4 to find the second term of the quotient using the same mantra.
The procedure should be repeated until a remainder is acquired. This could be zero or have a variable power that is less than that of the divisor. You will get a remainder equal to zero if the divisor is a dividend factor. You will get a remainder whose degree is less than the divisor’s if the divisor is not a factor of the dividend.
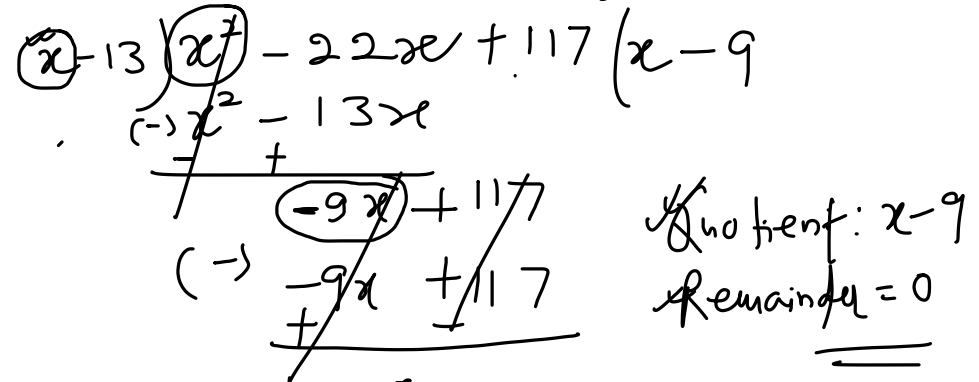
Factorize the expressions and divide
Mantra: You can factorize the expression using any method you have studied like split mid-term or using identity.
Step 1: Using any factorization technique, factorize the dividend and divisor (if applicable) step-by-step.
Step 2: After obtaining the factors for the provided expressions, you must eliminate the common factors that are present in both the denominator and the numerator.
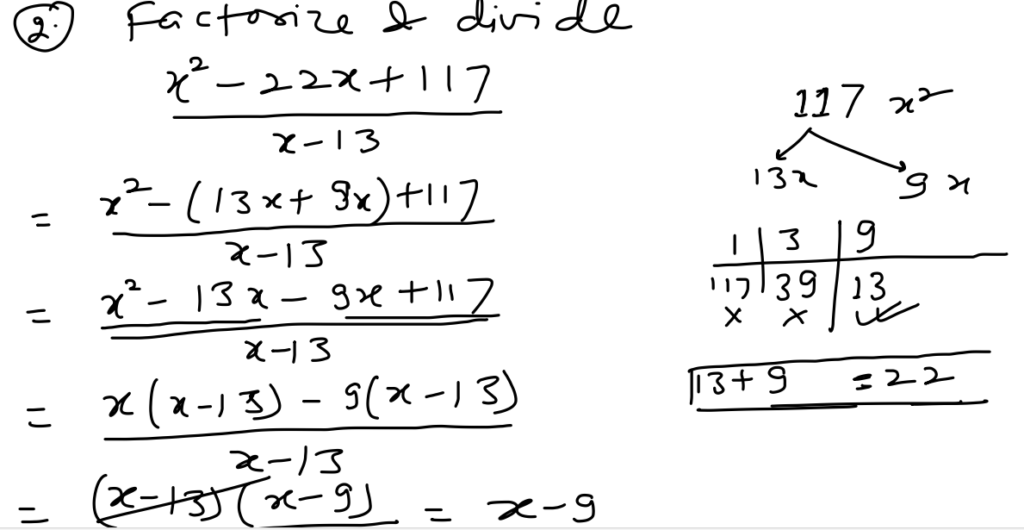
Polynomial-based equations can be solved and expressions made simpler with the use of algebraic division. It is crucial to remember that practice makes perfect, and the ideal method for mastering algebraic division is to practice a ton until you can complete the examples correctly each time.
Significance Of Algebraic Division
One of the key concepts in algebra is polynomial division. It is used to divide two polynomials and find their quotient. Algebraic division is significant for the reasons listed below.
Coding: Polynomial division is a useful tool in engineering, design, architecture, and a number of other practical fields.
Error detection: In error-control coding theory and practice, polynomial long division is utilized. Through the application of cyclic codes, errors are detected.
Factoring: The process of determining if a polynomial has a factor and, if so, figuring it out using long division.
Divide Polynomial in 7 seconds using Synthetic Division: A shorthand method to divide polynomials by linear factor of the form (x-a), where constant a is possible roots of the polynomial.
Synthetic division is a method used to divide polynomials. It is a shorthand method that simplifies the process significantly but can only be used when dividing by a linear factor (the divisor is a linear factor). It can also be used to factor polynomials. It is faster and simpler than long division and uses fewer calculations.
Steps to perform synthetic division:
Step 1: Write the polynomial in standard form, with the terms arranged in descending order of degree.
Step 2: Identify the divisor, which must be a linear factor of the form (x – a).
Step 3: Write the coefficients of the polynomial in a row, leaving a space for the constant term.
Step 4: Write the value of ‘a’ outside the row of coefficients.
x-13 = 0 => x = 13; So, a = 13
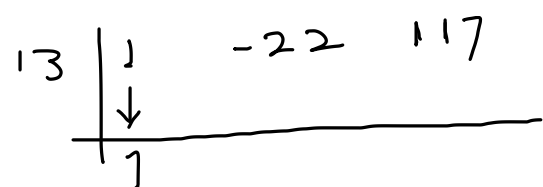
Step 5: Bring down the first coefficient of the polynomial.
Step 6: Multiply the value of a by the coefficient you just brought down and write the result under the next coefficient.
Step 7: Add the two numbers you just wrote down.
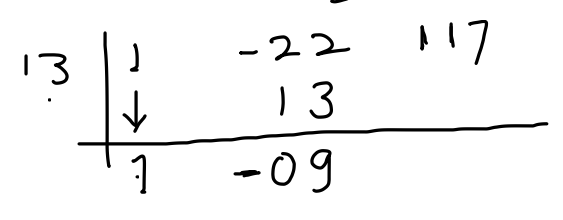
Step 8: Repeat steps 6 and 7 until you reach the last coefficient.
The final result is the quotient of the division, with the remainder written over the divisor.
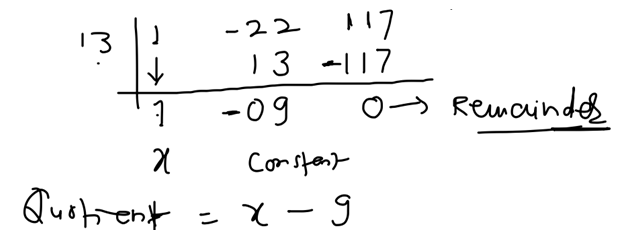
Another Example:
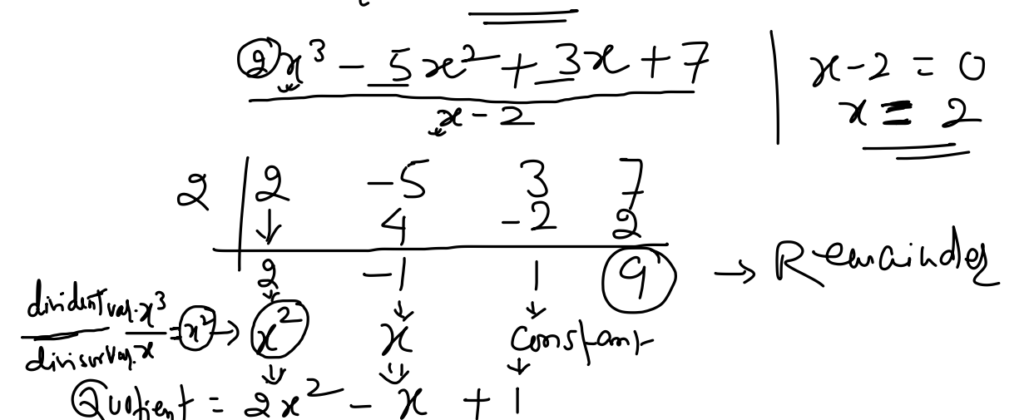
Frequently Asked Questions on Synthetic Division
When Can You Use Synthetic Division?
Synthetic division is a useful tool for dividing polynomials, especially when the divisor is a linear factor. It can be used to find the zeroes of polynomials, evaluate polynomials, simplify polynomial division, and factor polynomials.
Why is Synthetic Division Important?
Synthetic division is an important tool in algebra that simplifies polynomial division, finds the zeroes of polynomials, evaluates polynomials, factors polynomials, and saves time and space.
What Is Synthetic Division’s Primary Use?
Synthetic division is mostly used to divide polynomials in an easy and straightforward manner, particularly when the divisor is a linear component. The following are a few major applications for synthetic division:
Polynomial zero finding: The zeroes of a polynomial equation can be found using synthetic division. The divisor is a factor of the polynomial equation if the remainder is zero, and the remaining factors can be found using the quotient that results from synthetic division.
Polynomial evaluation: Polynomials at a given value of x can be evaluated via synthetic division. The polynomial is divided by (x – a), where an is the value at which the polynomial is to be assessed, to achieve this. It is the value of the polynomial at x = a that is produced as the residue after synthetic division.
Polynomial division made simpler: Dividing a polynomial by a linear factor is known as synthetic division. It is a quicker and easier way than long division because it involves less calculations and writing.
Factoring polynomials: A polynomial equation can be factored via synthetic division. The quotient obtained through synthetic division can be factored further using several techniques if the divisor is a factor of the polynomial equation.
In conclusion, synthetic division is a practical method for splitting polynomials, particularly in cases when the factor being divided is linear. It can be used to factor polynomials, evaluate polynomials, identify the zeroes of polynomials, and simplify polynomial division.
